Zhonghan Wang

zhece.wang@mail.utoronto.ca

I am currently working as an Algorithm Engineer (Machine Learning Engineer, MLE) at Baidu, focusing on large language models and intelligent agent systems. I have also received a Ph.D. offer in Electrical and Computer Engineering from The Edward S. Rogers Sr. Department of Electrical and Computer Engineering at the University of Toronto, which is currently deferred due to visa processing. Earlier, I earned my B.Eng (2021) in Electrical Engineering from Nankai University, and M.Eng (2025) in Computer Science from the Institute of Software, Chinese Academy of Sciences.

My current research interests lie at the intersection of large language model reasoning, mathematical theorem proving, and AI systems, with both academic and industrial perspectives.

  1. LLM reasoning and mathematical theorem proving, including enhancing reasoning capabilities of large language models, integrating formal methods with neural approaches, and improving performance on complex mathematical and logical tasks.
  2. Agent systems and post-training of LLMs, focusing on building intelligent agents with tool-use capabilities, and improving model performance through supervised fine-tuning (SFT) and reinforcement learning (RL).
  3. Formal methods and automated reasoning, including SMT solving, nonlinear arithmetic, and exploring their interaction with modern AI systems.

[New] I am open to academic collaborations and industry opportunities. Please feel free to contact me if you would like to explore any potential cooperation.

CV  |  Google Scholar  |  LinkedIn  |  Github  |  ORCID  |  Blog

profile photo


Publication ( Show Selected / Show All by Date ) 🔬

SMT Solving

Complete Method

Incomplete Method / Local Search

(*): Equal contribution

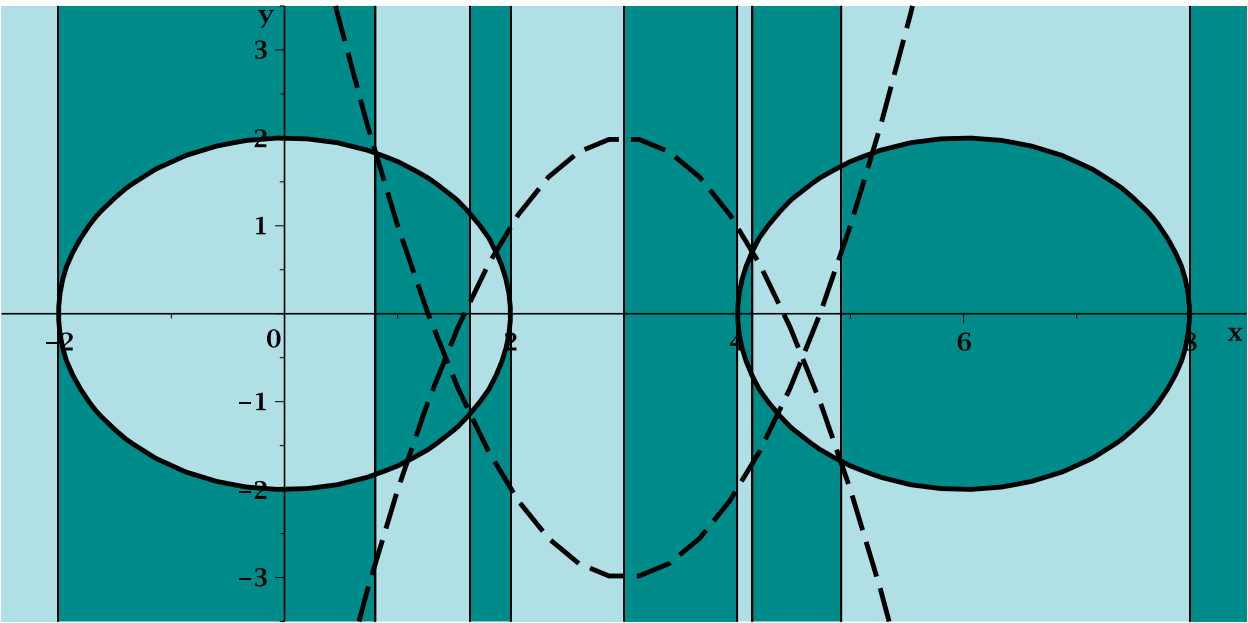
Improving NLSAT for Nonlinear Real Arithmetic
Zhonghan Wang
[ASE 2025]
The 40th IEEE/ACM International Conference on Automated Software Engineering

arXiv | code | paper | poster | slides | video |
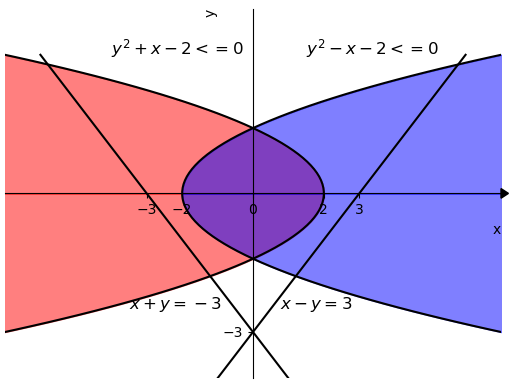
Efficient Local Search for Nonlinear Real Arithmetic
Zhonghan Wang, Bohua Zhan, Bohan Li, Shaowei Cai
[VMCAI 2024]
The 25th International Conference on Verification, Model Checking, and Abstract Interpretation

arXiv | code | paper | slides | video |

Intern Experience 🚀
Oct 2022 - Aug 2023 Alibaba Group – Alimama Advertising Technology Department, Beijing, China
Algorithm Intern
Worked on constrained optimization for large-scale ad allocation using local search–based methods. Modeled allocation as a constrained optimization problem with hard constraints (e.g., budget, feasibility) and soft constraints (e.g., CTR, CVR, competition coefficients). Designed efficient search strategies and objective formulations to balance multiple business metrics and improve overall system performance.
Nov 2025 - Present Ant Group – Ant Digital, Hangzhou, China
Algorithm Intern
Worked on supervised fine-tuning (SFT) and reinforcement learning for large-scale prover models. Designed fine-grained, rubric-based reward signals (e.g., correctness, step validity, reasoning strategy) to improve RLHF stability and performance. Built a distributed RL training pipeline across multiple machines (rollout and training nodes). Developed data pipelines for Lean-based formal proofs, enabling scalable training and improving model performance on formal reasoning tasks.
Service 🤝
Artifact Evaluation Committee VMCAI 2025
Selected Awards 🎉
Gold medals of Z3++ in SMT-COMP QF_NRA Single Query (main developer) (2022, 2023)
Globalink Research Internship offer (Alberta University, Canada) (2020)
Outstanding Prize for Tianjin College Student Mathematical Competition (Ranked 17) (2018)
Travel Gallery 💫
London 2024 (POPL) Google Photos
Seoul 2025 (ASE) Google Photos
Visitors

Template adapted from 1, 2, 3 and 4.